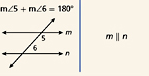3.3 : Proving Lines Parallel
Theorems and Postulates:
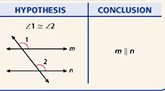
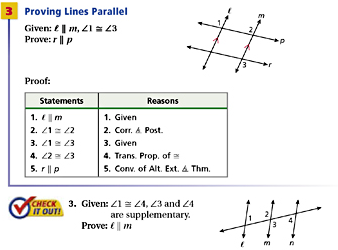
Converse of the Corresponding Angles Postulate- If two coplanar lines are cut by a transversal so that a air of corresponding angles are congruent, then the two lines are parallel.
Theorems and Postulates:
Converse of the Corresponding Angles Postulate- If two coplanar lines are cut by a transversal so that a air of corresponding angles are congruent, then the two lines are parallel.
Parallel postulate- Through a point P not on line l, there is exactly one line parallel to l.
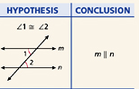
Converse of the Alternate Interior Angles Theorem- If two coplanar lines are cut by a transversal so that a pair of the alternate interior angles are congruent, then the two lines are parallel.
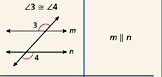
Converse of the Alternate Exterior Angles Theorem- If two coplanar lines are cut by a transversal so that a pair of the alternate exterior angles are congruent, then the two lines are parallel.
Converse of the Same-Side Interior Angles Theorem- If two coplanar lines are cut by a transversal so that a pair of the same-side interior angles are supplementary, then the two lines are parallel.
Examples: