4.5 Triangle Congruence: ASA, AAS, and HL
Definitions:
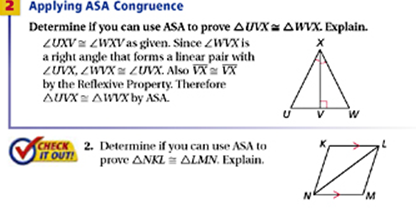
Included Side - the common side of two consecutive angles in a polygon
Postulates/Theorems:
Angle-Side-Angle (ASA) Congruence Postulate - If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent
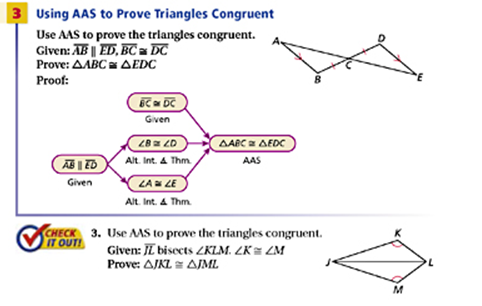
Angle-Angle-Side (AAS) Congruence Theorem - If two angles and a non-included side of one triangle are congruent to the corresponding angles and non-included side of another triangle, then the triangles are congruent
Hypotenuse-Leg (HL) Congruence Theorem - If the hypotenuse and a leg of a right triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangles are congruent
*Note: If you have trouble remembering which are postulate and which are theorems look at the letter pattern. ASA, SSS and SAS are all postulates and the letters all have a symmetry about them. AAS and HL have no pattern and they are the theorems.
Examples:
Definitions:
Included Side - the common side of two consecutive angles in a polygon
Postulates/Theorems:
Angle-Side-Angle (ASA) Congruence Postulate - If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent
Angle-Angle-Side (AAS) Congruence Theorem - If two angles and a non-included side of one triangle are congruent to the corresponding angles and non-included side of another triangle, then the triangles are congruent
Hypotenuse-Leg (HL) Congruence Theorem - If the hypotenuse and a leg of a right triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangles are congruent
*Note: If you have trouble remembering which are postulate and which are theorems look at the letter pattern. ASA, SSS and SAS are all postulates and the letters all have a symmetry about them. AAS and HL have no pattern and they are the theorems.
Examples: